A common criticism gainst economics is that it uses incomprehensible math language to describe itself, as if that’s the true reason a bunch o’ rich academics prefer philosophies that benefit rich academics. ‘Cause we know from the Tea Party Movement that plain ( AKA sloppy ) language ne’er leads to sloppy economics ( i.e. economics I don’t believe in ).

Mo’ wary economists acknowledge that math language isn’t necessary for economics, but has 2 benefits:

• It’s mo’ rigorous than plain language, & thus harder to make invalid statements ( though it’s still possible — not to mention that this does nothing to protect gainst inaccuracy ).

• Economists being, well, economists, can understand it better than your human language with all its gooey emotions.

There’s something to say ’bout the 1st point. Austrian-schoolers famously claim that math language isn’t necessary ( though can’t argue why it’s necessary not to have it ), & then hurt their cause by having a much sloppier logical system¹ with vague language, logical jumps, & outright inaccuracies ( despite Mises’s claim that praxeology only makes abstract logical statements )².

So I’m recommending a different solution: replace math language with programming language. Economists can’t claim the 1st point gainst this solution: the fact that computers can run off programming language is proof that it’s mathematically rigorous. But I’d also argue that it’s much mo’ readable than math language, if done right.

Indeed, unlike math, programmers take the readability o’ code very seriously. This is ’cause o’ a fact ’bout programming that most people probably don’t realize: that it’s aimed @ writing for humans, not computers. This makes sense: programmers rather quickly realized that they can create computer programs — “compilers” or “interpreters”, depending on how it’s used — that can translate text into machine code.

Now, this obviously has limits.³ ‘Cause human languages are vague, plain English can’t be used; but different languages heavily inspired by English can be used, albeit with much stricter grammar & diction rules than human languages.

Keynes.js

I’ll use Keynes’s General Theory as an example, since ’twas what 1st inspired this view. Keynes, like any economist, loves incoherent math formulae. I’ll go through its primary flaw: wording.

Calculus has this odd pattern o’ using single letters, or e’en Greek letters, to represent concepts & values & a letter plus a letter in parentheses afterward to represent functions. This has greater advantages than being incomprehensible to anyone who doesn’t memorize them: they’re also super hard to position & configure on computers. ¿Isn’t smothering characters in some big E with angled ends — called “Sigma E” — much mo’ elegant than boring ol’ “function SumOFunctionOutputsFromInputInterval( first_number, last_number, function )”.⁴

It’d be nonsense to argue that economists can’t use words ’cause they’re too vague, but that they can use just letters & symbols, which are e’en less meaningful. The fact that computers can run logically-consistent programs with words proves that economics can, too, so long as it uses these words as precisely & consistently as programs.

The trick is to set off variable names ( function names should already be easy to distinguish from plain English ), — maybe bold them — define them precisely when 1st using them ( in programming, we call this “initialization” ), & ne’er use them for anything else. Don’t use them in the description text @ all; treat doing so as trying to create ‘nother variable with the same name, which would create a compilation error.⁵

To give an example, let’s take the formula from the beginning o’ Book III o’ General Theory:

C_w = χ(Y_w) or C = W * χ(Y_w)

I want to point out that this formatting in my copy is so bad that I’m not e’en sure if I got this formula accurate. I’m not sure if that asterisk is s’posed to be there or if it’s some obscure math meaning ( using the same symbol for different functions is less common in math than one might expect from such a rigorous science ) or if it’s just a printer smudge. It’s slightly off-center, which is suspicious. Also, Keynes just mashes “I can’t believe it’s not χ” & the parenthetic expression next to it to form multiplication earlier, ¿so why not just mash W & χ together?

Basically, I’m going to want to append this image next to Keynes’s formula:

Yeah, this is called a “coding horror”. If you click that link you may see an article that proves that, though economists should talk like programmers, programmers probably shouldn’t talk ’bout politics, ’cause they might look silly ( yes, I could totally imagine a programmer with no experience in politics winning a local election based purely on his disgust with the current president — as if that’s a rare commodity — & his inability to tell that election system from Stack Overflow )⁶. Anyway, this icon is actually from a book called Code Complete, by some other guy & is used to set out particular awful pieces o’ coding, much as blogs set out particularly awful wording with bold. I’d recommend reading that book, since it talks ’bout the comprehensibility issues I’m talking ’bout in greater depth. I’d recommend Clean Code & Cleaner Code e’en mo’.

Anyway, let’s make this fomula not suck:

Let’s start by noticing that these 2 formulae are probably the same, ‘cept spelled-out in needlessly opaque ways. C_w is “consumption based on `wage units'” Let’s ignore that the “propensity for consumption” is apparently based mainly on lowly wages & just focus on translating. C is just “consumption”, & is = to the same thing, but multiplied by uppercase W. If one reads “The Choice of Units”, which I don’t recommend, one will learn that W is — surprise — “wage units”, which I believe is the average wage money per worker. ( I just know it’s some form o’ “wages” / some # o’ workers. Keynes is terrible @ specifying domains, but common sense tells me he’s talking ’bout a country’s economy. Since none o’ this is backed by any evidence or data, it doesn’t matter anyway. It could apply to the Gusty Glade Galaxy for all we care. ) So… basic math tells us that C_w = C/W. So, C_w must be average consumption per average wage.

Thus we have our 2 functions:

function AverageConsumptionPerAverageWages( χ, Yw )

function TotalConsumption( average_wage, χ, Yw )

Already, things are looking much mo’ coherent.

Thankfully, these 2 functions share the same 2 variables. As it turns out, I realized that these weren’t 2 variables being multipled together, but 1 other function with Y_w as an argument. These are the kind o’ parsing errors you still have to look out for in programming. For instance, in C++, it’s still possible for a compiler to mistake the initialization o’ a variable through parentheses with the initialization o’ a function.

So… ¿I guess C_w & C are variables to functions? Good thing that works perfectly for JavaScript:

var AverageConsumptionPerAverageWage = function( Y_w ) {};

var TotalConsumption = function( average_wage, Y_w ) {};

Let’s just appreciate how much easier it is to understand the word “function” o’er a cheap knock-off version o’ the letter “χ”.

Now we just need to figure out Y_w. I’ve figured it out: it’s “income in terms o’ wage units”, which is a weird way o’ saying “income per wage unit”, which is a weird way o’ saying “income per average wage”.

Thus, now we have:

var AverageConsumptionPerAverageWage = function( income_per_average_wage ) {};

var TotalConsumption = function( average_wage, income_per_average_wage ) {};

Note that average_wage & income_per_average_wage could be described as functions, too:

var AverageWage = function( total_wages, total_number_of_employees) {};

var IncomePerAverageWage = function( total_income, AverageWage ) {};

Now, we still need to define the implementation o’ these functions. We already know AverageWage & can easily discern IncomePerAverageWage through that:

var AverageWage = function( total_wages, total_number_of_employees )
{
    return total_wages / total_number_of_employees;
};

var IncomePerAverageWage = function( total_income, average_wage )
{
    return total_income / average_wage;
};

Thus, we’d call IncomePerAverageWage thus:

var income_per_average_wage = IncomePerAverageWage( total_income, AverageWage( total_wages, total_number_of_employees ) );

In contradiction to my core claim in this article, there’s a difference ‘tween total_income in this function call & in the function definition earlier. In programming, this is known as “scope” ( sort o’ like my namespace point made in a footnote down below ). The total_income in the function definition only exists for the duration o’ that function call & is set to whatever is pushed to it through this call. This call, meanwhile, references a specific variable whose scope we’ll deal with later.

Anyway, we have 2 mo’ functions to define:

var AverageConsumptionPerAverageWage = function( income_per_average_wage )
{
    return income_per_average_wage;
};

‘Course, this 1 is pointlessly redundant ( & a wrong assumption ).

var TotalConsumption = function( average_wage, income_per_average_wage )
{
    return average_wage * income_per_average_wage;
};

Interestingly, we could redefine AverageConsumptionPerAverageWage in a ( slightly ) mo’ meaningful way.

var AverageConsumptionPerAverageWage = function( total_consumption, average_wage )
{
    return total_consumption / average_wage;
};

‘Course, comparing these 2 functions & understanding basic math will allow one to see that total_consumption / average_wage will inevitably = income_per_average_wage — which is, ‘course, the whole point ( mo’ on this later ). That average_consumption isn’t a particularly meaningful value — better median_consumption — is beyond our scope.

Here we can see all the pieces together:

var TotalConsumption = function( average_wage, income_per_average_wage )
{
    return average_wage * income_per_average_wage;
};

var AverageConsumptionPerAverageWage = function( total_consumption, average_wage )
{
    return total_consumption / average_wage;
};

var AverageWage = function( total_wages, total_number_of_employees )
{
    return total_wages / total_number_of_employees;
};

var IncomePerAverageWage = function( total_income, average_wage )
{
    return total_income / average_wage;
};

var total_income = 16770; // In billions. // These 2 must be
var total_wages = 157.5; // In billions. // in the same unit.
var total_number_of_employees; = 124.73    // In millions.

var average_wage = AverageWage( total_wages, total_number_of_employees );
var income_per_average_wage = IncomePerAverageWage( total_income, average_wage );

var total_consumption = TotalConsumption( average_wage, income_per_average_wage );

console.log( total_consumption ); // Prints 16770 to browser debug console.

Mo’ Fun

You’ve probably noticed by reading the comment after the final statement or running this code yourself ( you can make the debug console pop up in most browsers by pressing F12 ) that total_consumption = total_income. While just following the logic o’ the functions & understanding basic math shows this, familiarity with economics & basic pattern-recognition was mo’ an asset.

But with programming languages, we have 1 tool we can use to test this a lot: conditionals.

To simplify, let’s wrap up the code outside o’ functions in the previous program into 1 big function & have it return a value:

var TotalConsumptionFromIncomeWagesAndEmployees = function( total_income, total_wages, total_number_of_employees )
{
    var average_wage = AverageWage( total_wages, total_number_of_employees );
    var income_per_average_wage = IncomePerAverageWage( total_income, average_wage );

    return TotalConsumption( average_wage, income_per_average_wage );
};

This’ll abstract ‘way all these connections so we don’t have to go through them ‘gain.

Let’s add 2 mo’ functions. The 1st is a simple helper function:

var RandomNumber = function()
{
    var MAX = 99999999999999;
    return ( Math.random() * MAX );
};

JavaScript’s built-in random function is odd: it returns a random # ‘tween 0 & 1. This function increases that to 99.9… trillion.

The next function is the main focus o’ this program:

var TestThatConsumptionEqualsIncome = function( iterations )
{
    var total_income;
    var total_wages;
    var total_number_of_employees;
    var total_consumption;
    
    var consistent = true;

    if ( isNaN( iterations ) ) // isNaN: Not a #
    {
        iterations = 999; // Default
    }
    
for ( var i = 0; i < iterations; i++ )
{
    total_income = RandomNumber();
    total_wages = RandomNumber();
    total_number_of_employees = RandomNumber();
    
    total_consumption = TotalConsumptionFromIncomeWagesAndEmployees
    (
        total_income,
        total_wages,
        total_number_of_employees
    );
        
    if ( total_consumption != total_income )
    {
        consistent = false;
    }
}
    if ( consistent )
    {
        console.log( “¡Our math formulae are pure!” );
    }
    else
    {
        console.log( “¡Economics is a failure! ¡Abort!” );
        SmashCapitalism();
    }
};

1 major flaw o’ JavaScript is its lack o’ argument defaults ( values that the argument becomes if nothing is sent to the function in its place ). This is bewildering, since just ’bout every language has them, including the languages that were JavaScript’s main inspiration.

In this case, the need to manually check for a given argument isn’t too bad, since we need to ensure that it’s a #, anyway — which can’t be done automatically without static typing.

Anyway, now we just need 1 statement @ the end:

TestThatConsumptionEqualsIncome();

Run & let’s see the magic:

…

…

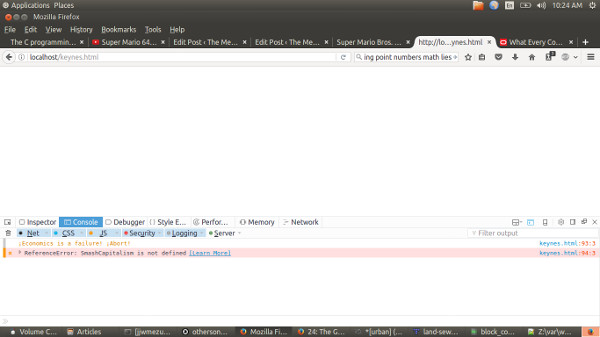
Math is a lie.

( Also, Firefox shows a hilarious depth o’ social knowledge with that line, “ReferenceError: SmashCapitalism is not defined”. )

All right, calm down. I tested this program a bit & realized that a’least 1 kind o’ math is a lie: floating-point #s. Try to ne’er use floating-point #s if you can; they can’t seem to understand such obscure, arcane concepts o’ equality. Looking @ the values gotten, total_consumption & total_income vary by .00000000001 or so. But e’en if they didn’t, they could fail equality, ’cause floating-point #s. This is the case wherein JavaScript’s loose typing is a pain — just like how I have to be careful doing math in Python so it doesn’t try to trick me into thinking 8 / 5 = 1. In C++ or Java I wouldn’t have this problem, ’cause they demand you specify the type. Then ‘gain, C++ also automatically converts types without you knowing, so it kind o’ sucks, too.

The problem is, trying to fix this is mo’ complicated than just wrapping Math.round() round every division. In my tests, ’twas strikingly common for these divisions to give 0 values ( which makes sense, since it’ll be common for the values to be close ‘nough that division would give some value below .5 ) & when a # was divided by 0, which every mathematician knows is kosher, it gives “Infinity”. & when that’s multiplied, we get “NaN”. In that case, we’re guaranteed to get an economic disaster, since NaN isn’t equal to anything — e’en itself. Now, this is what I call a well-designed programming language.

Obviously I can’t just do bounds-fixing for 0, since that would change data, which could cause values to go out o’ sync & cause the same capitalism-destroying problem. Also, fixing our “model” by just “fixing” the data is both hilariously wrong & yet hilariously right for an economist.

Thankfully, I have a much mo’ elegant way to move the goalposts — 1 that’s, if I say so myself, much saner: we’ll just change the definition o’ “=”:

var AbsoluteDifference = function( one, two )
{
    return Math.abs( one – two );
};

var CloseNough = function( one, two )
{
    // I said, “¡Hey! ¿Are we doing government work here?”
    return AbsoluteDifference( one, two ) < 1;
};

By the way, if you e’er hope to get a job programming, I highly recommend you fill your functions with silly comments that reference songs & memes & stuff. I can guarantee your boss’ll think you have the utmost professionalism.

Interestingly, the new ES6 standard apparently has some Number.EPSILON variable that is s’posed to be used for comparing floating-points, rather than using a better # system. ‘Cept, that # doesn’t seem to work with my program ( probably ’cause o’ all the divisions that lead to further impurities ).

& now we change change the conditional statement:

if ( !CloseNough( total_income, total_consumption ) )
{
    consistent = false;
}

Let’s see how it works now:

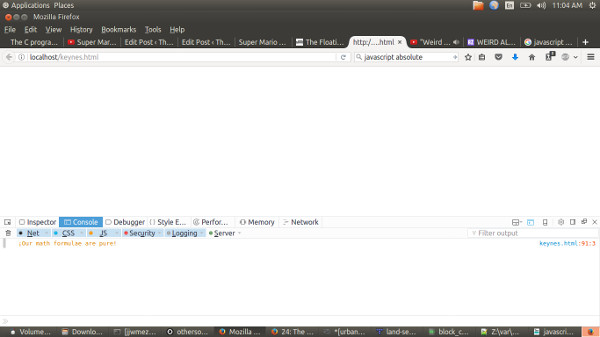
( Holds breath ).

¡Capitalism is saved!

¿Why’d I waste my time on this horse-piss ‘gain?